絵を描いて説明すると伝わりやすいことがあります。
せっかくなら違和感のない絵が描けると、相手が説明を聞くのに集中できます。
ということで、今回は違和感なく立方体を描くコツを書きます。
「立方体を描く場面なんてあるのか?」という疑問は横に置いておきます。
すべての形の基本は立方体!!!
立方体が素早く立体的に描けたらかっこいいよね!!!(強引ですが)
なお、人に素早く描いて伝えることを目的としているため、定規は使いません!!
話途中に定規が出てきたらかっこよくないので!!
フリーハンドで書いていきます!!
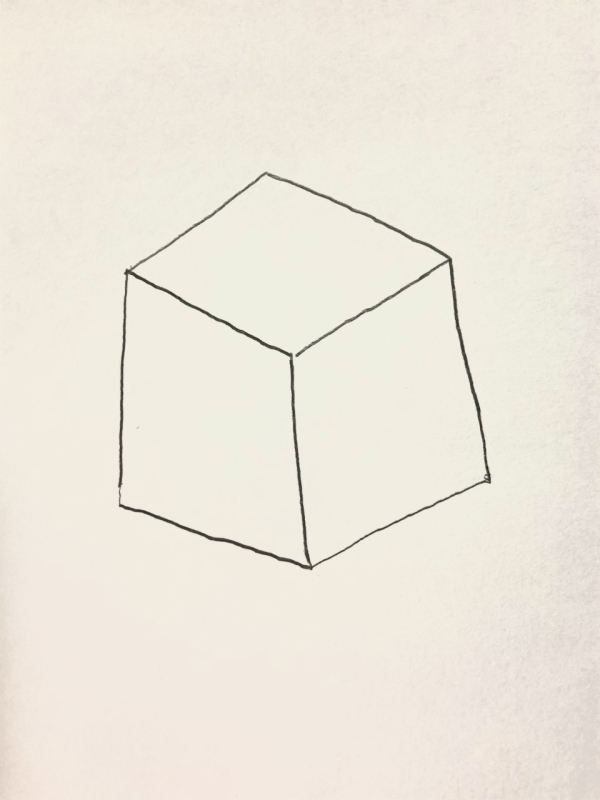
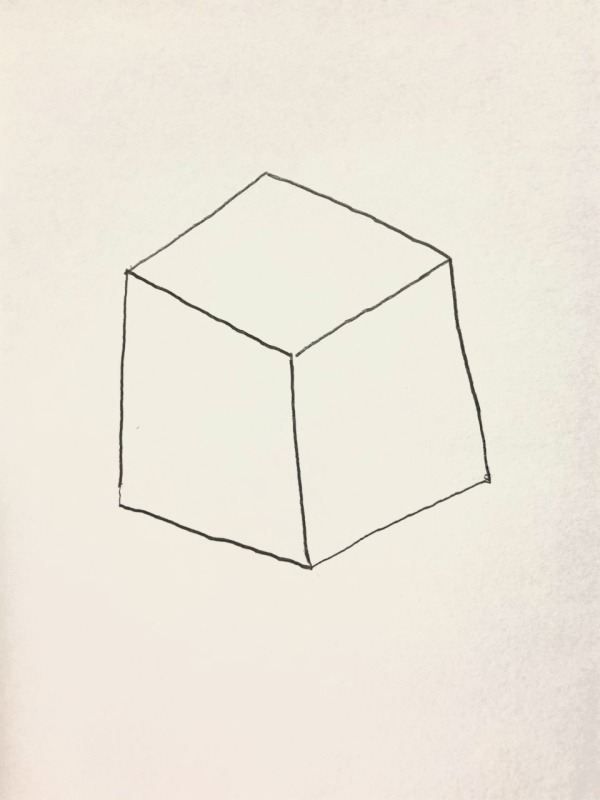
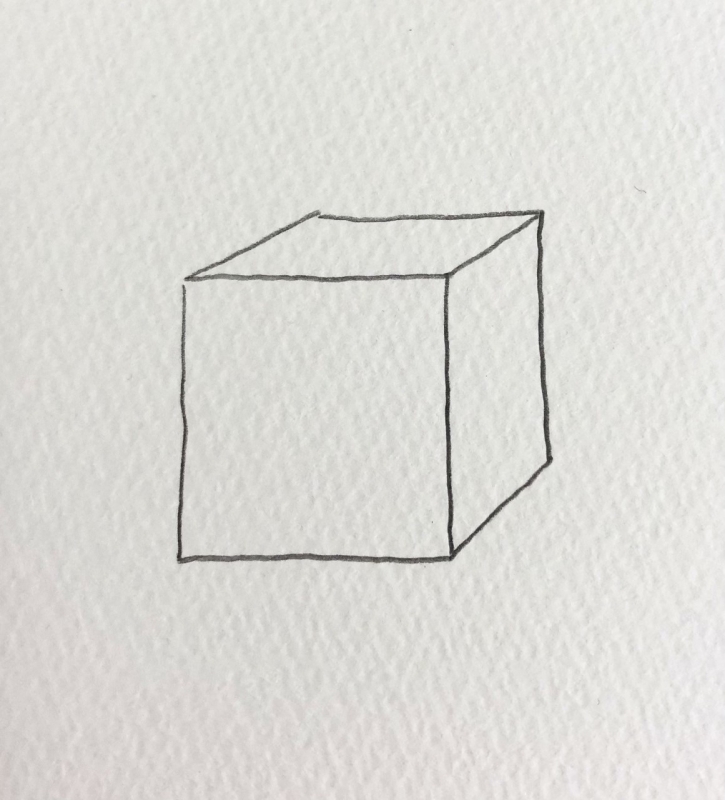
なんか変
この立方体はなんだか気持ち悪いですね。
話の途中でこの立方体が出てきたら、気になって話がしっかり聞けないかもしれません。。。。
なんで気持ち悪いかというと、遠近法のルールを無視して描いているからなんです。
今回は、3つの点透視図法による遠近法をご紹介します。
点透視図法(point-projection perspective)は消失点へ平行線を収束させることで遠近感を生む手法である。透視平面(視点の前に置かれた架空のキャンバス)と角度を持つ直線(面と平行でない直線)は奥行きをもつため、透視図へ射影した際に消失点へ収束する。そして同じ角度を持つ直線群すなわち平行な直線群は同一の消失点へ収束する。この事実に基づき消失点へ平行線を収束させる図法が点透視図法である。
一点透視図
〈一点透視図法〉
一点透視図法(英: one-point perspective)は1つの消失点へ平行線群を収束させる図法である[12]。平行線が1つの消失点へ放射線状に収束するように描かれる。透視平面と平行な面があり、その面から奥側へ平行線群が伸びるような構図の場合に1点透視図法を用いる。
Wikiに描かれている遠近法の文章が難しすぎて、絵がないと理解できない・・・。
ということで描きました。
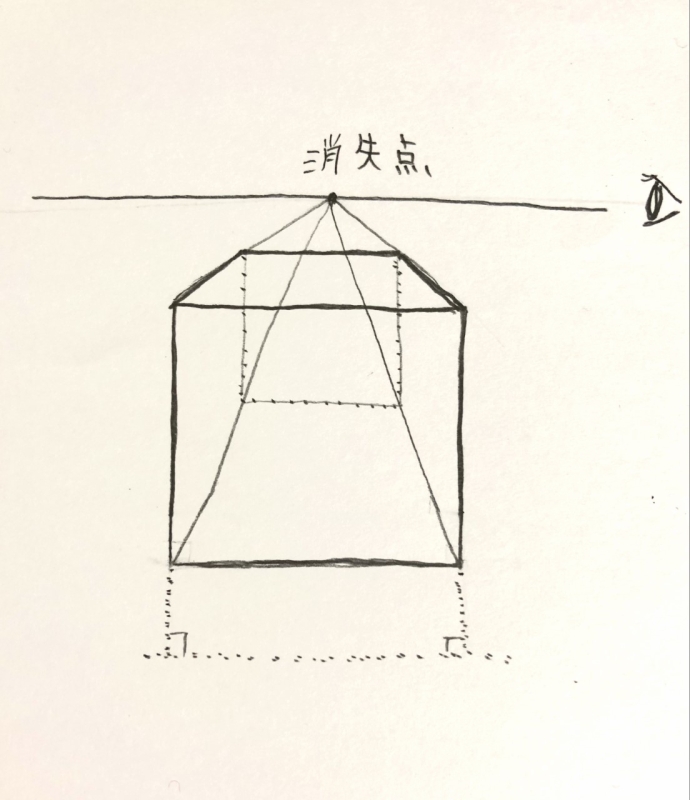
立方体を真正面から見た時に描く方法です。
正方形の角から消失点に向かって線が伸びていきます。
縦と横の線は水平垂直です。
消失点を目の高さと考えると良いかもしれません。
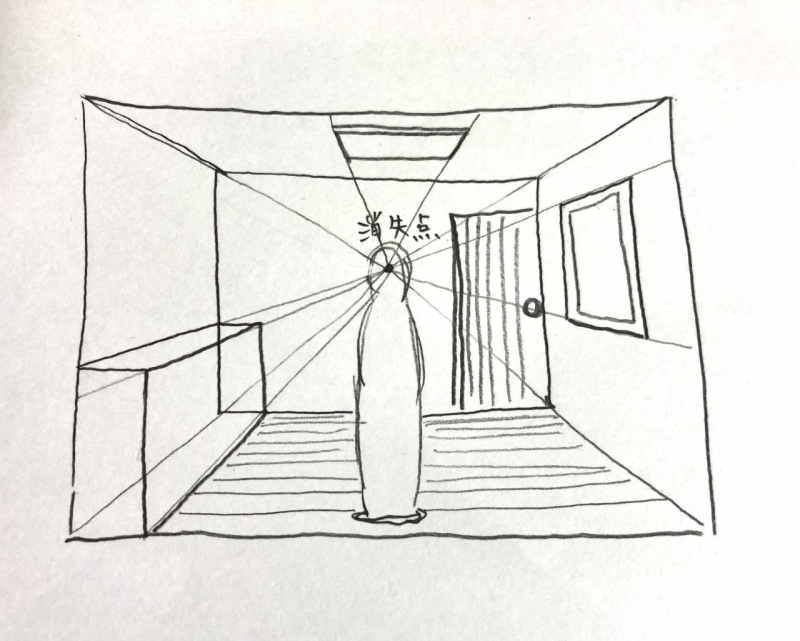
部屋の中などを表現する時に利用すると見やすいです。
二点透視図
〈二点透視図法〉
二点透視図法(英: two-point perspective)は角度が異なる2つの平行線群をそれぞれ消失点へ収束させる図法である。一辺が透視平面と平行で、それと交わる2つの直線が角度を持っている場合に用いられる。一点透視図法から視点を1軸回した場合(例: 建物を斜め横から見た場合)は2点透視図法になる。アイレベル(視線面)と平行な直線の消失点はアイレベル上に存在する。
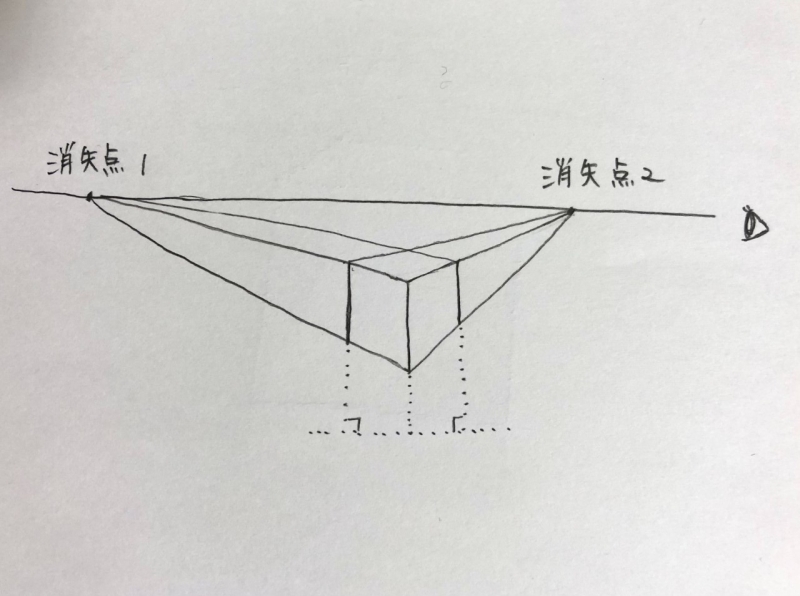
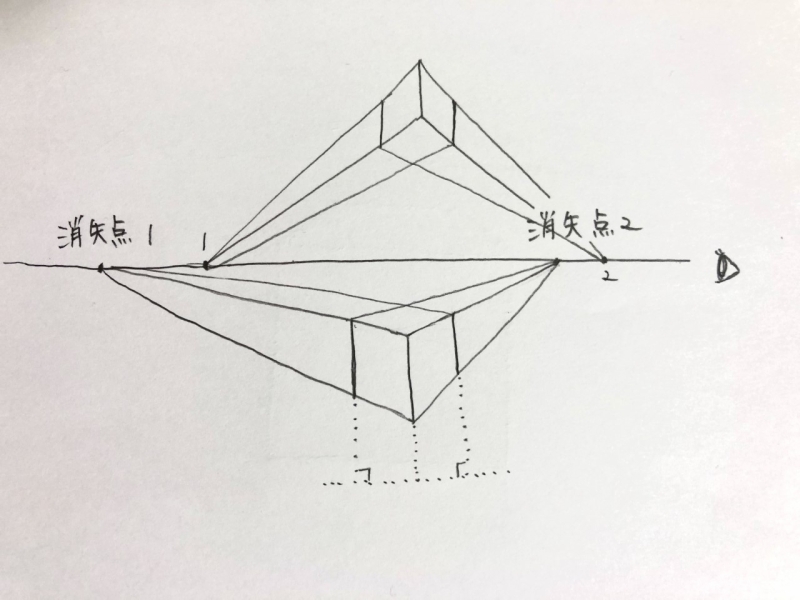
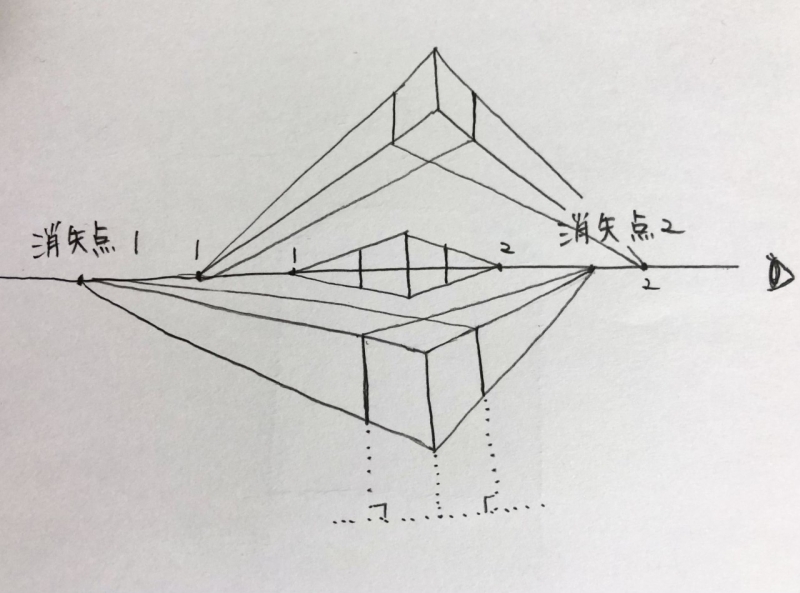
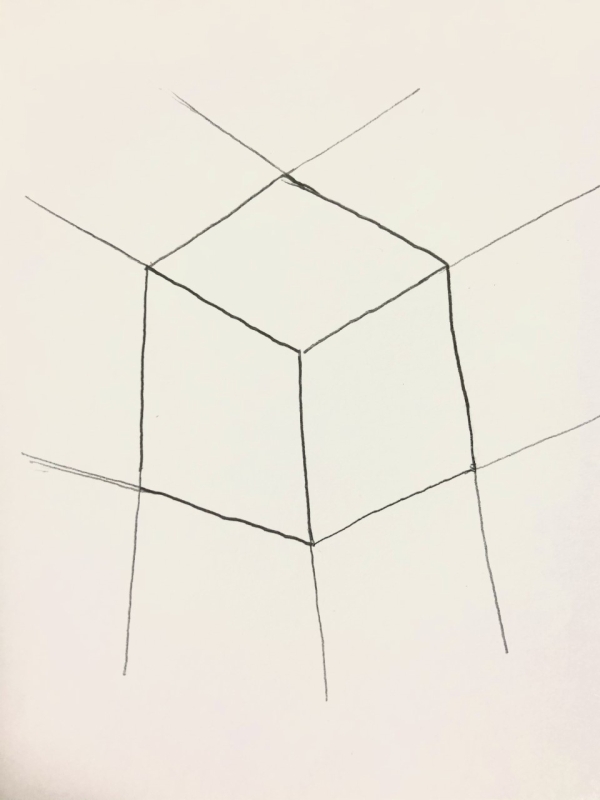
立方体を横方向に回転させて、見た時に描く方法です。
2つの消失点は水平です。
縦の線は垂直になり、左右の2つの消失点に向かって線が伸びていきます。
立方体は二点透視図法で描くと違和感なく描けます。
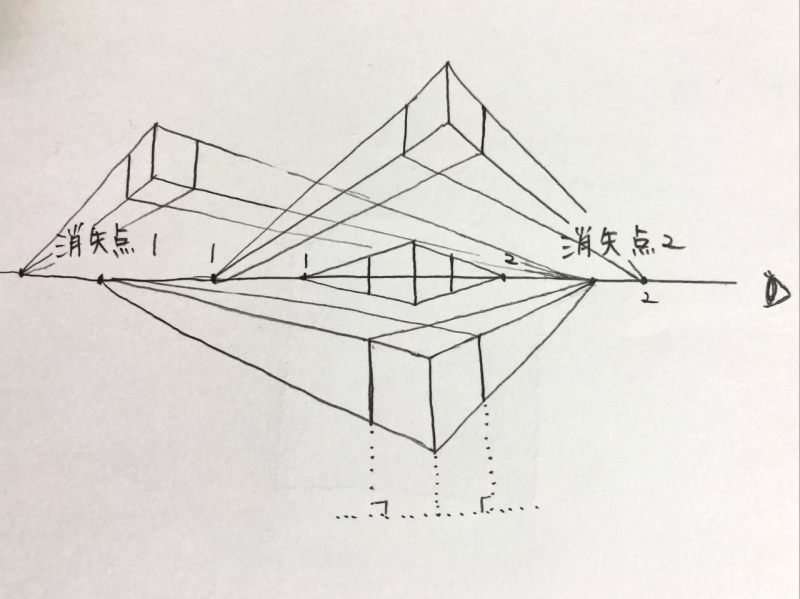
2つの消失点を水平移動させることで、回転した立方体を描くことも出来ます。
三点透視図
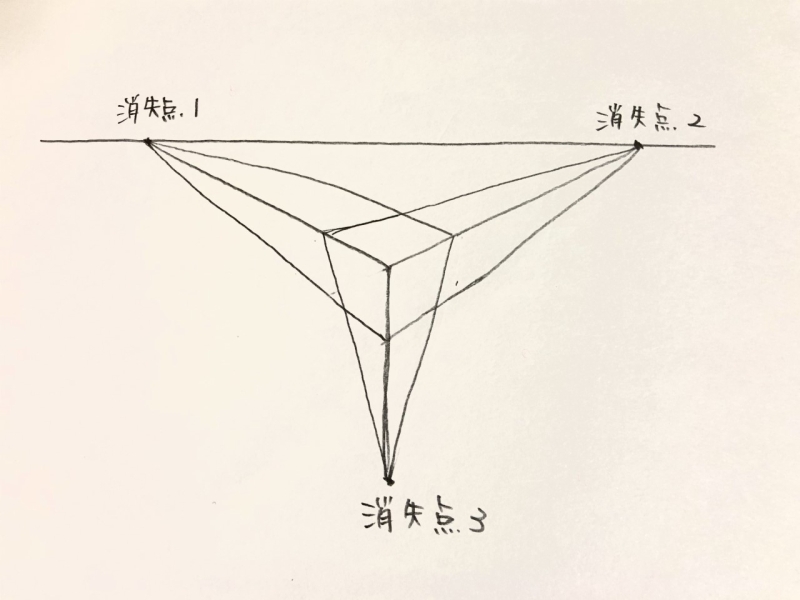
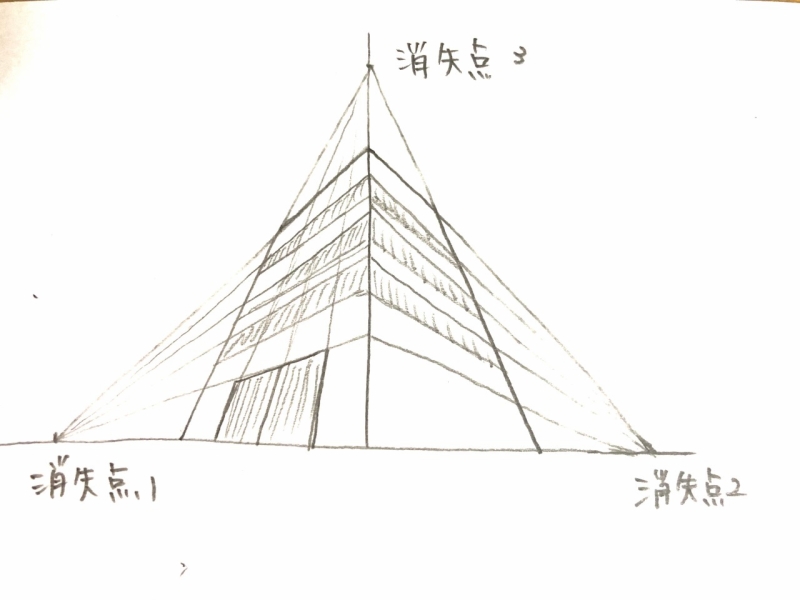
〈三点透視図法〉
三点透視図法(英: three-point perspective)は角度が異なる3つの平行線群をそれぞれ消失点へ収束させる図法である。立方体のどの辺も透視平面と平行でない場合は三点透視図法になる(例: 建物を斜め横から見たうえでさらに仰角・俯角をつけて見る)。
立方体を斜め下、または斜め上から見た時に描く方法です。
3つの消失点に向かって線が伸びていきます。
どの辺とも平行にはなりません。
高さや深さなどを表すときに利用すると良いです。
何が変だったのか?
最初の立方体の何が気持ち悪いと感じるか。
それは消失点に線が向かっていないことが原因でした。
今回の目的では消失点までの直線を描きませんが、意識しておくことは大切です。
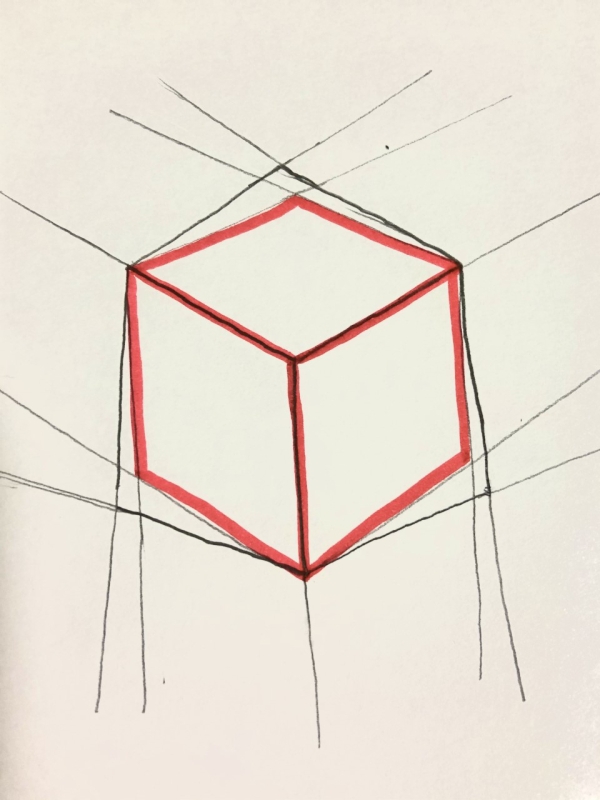
消失点とは逆方向に線が伸びると違和感のある立方体になります。
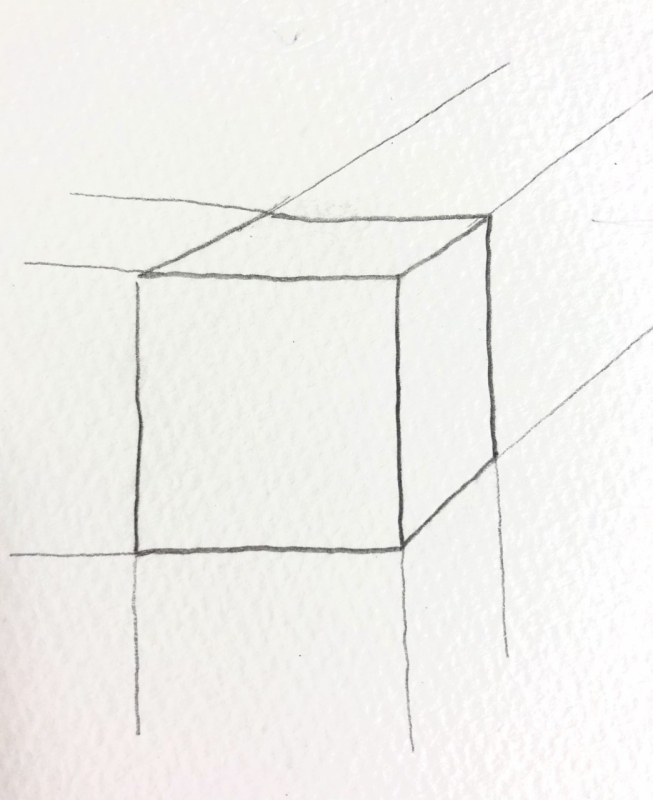
赤線で描き直したのは、二点透視図で描きなおした立方体です。
立方体だと思っていたら!!
小学校の算数の教科書で見たこの立方体も、遠近法のルールでみると立方体とは言えません。
線が消失点に向かわずに平行になっています。
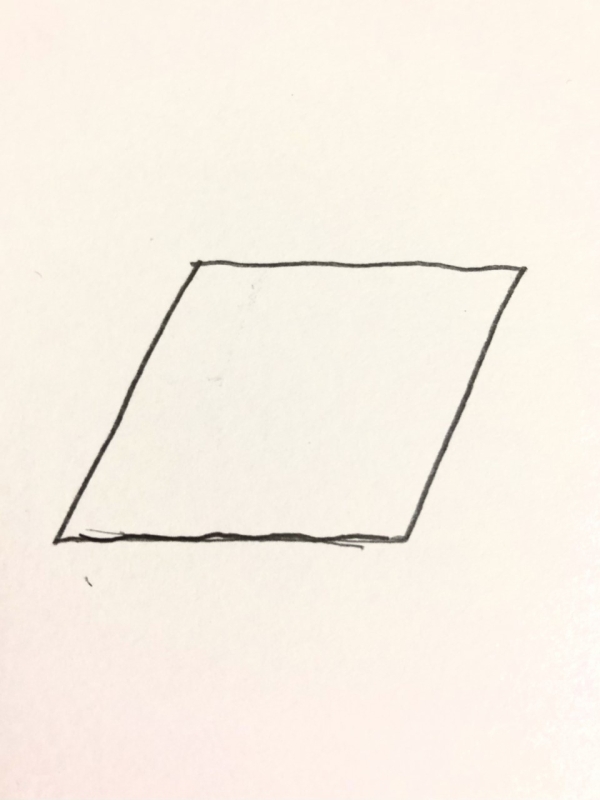
もしこの図形を上から見たら。。。。
平行四辺形になります。
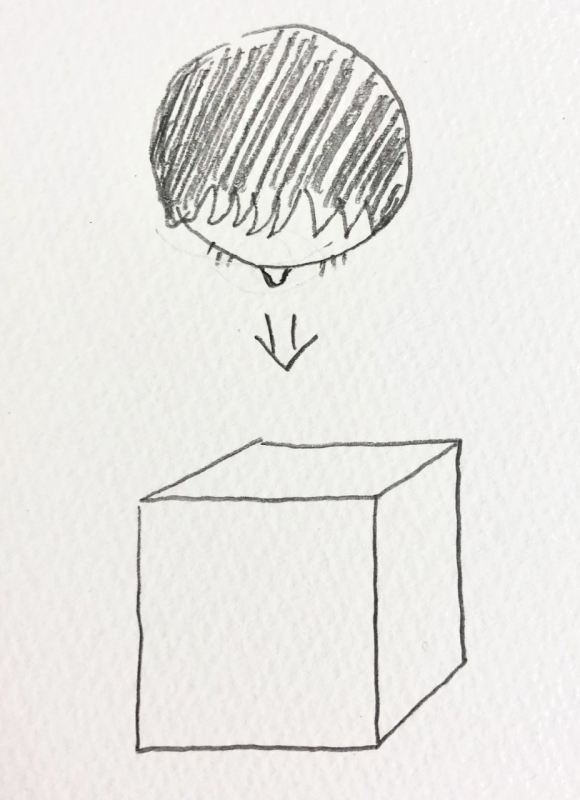
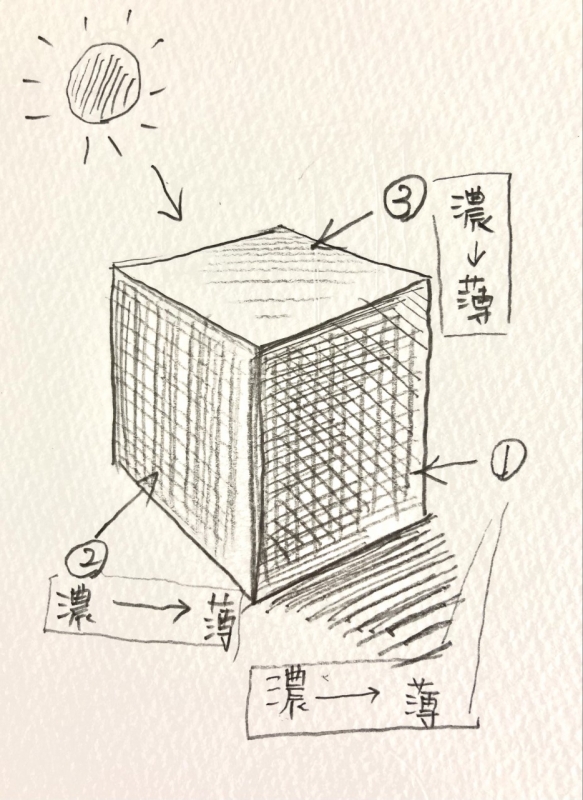
影をつけてみる
上手そうに見せるのならば、影をつけてみると「やるな」という雰囲気が出てきます。
①②③の順に色を薄くしていくと立体的になってきます。
更に面の中でも太陽に近いほど濃くしてグラデーションをつけるとちょっと上手そうに見えます。
多少汚くても、フリーハンドでちょっと説明するために描いているので良いんです。
まとめ
立方体の描き方のポイントが分かったら、なんだか描いてみたくなりませんか?
たかが立方体でも、使い所によって点透視図法を変えたり、ポイントを抑えて描くと見やすい仕上がりになります。
描けば描くほど熟れて上手くなるので、練習してみてください!
最終更新:
pamapama
すごくおもしろかったです。ちょうど、ちょっと前に好きな写真や映画のシーンには一点透視図法を駆使したものが多かったと知ったところだったのです。https://gigazine.net/news/20120901-kubrick-one-point-perspective/